i’m going to calculate this using the binomial distribution, where n = number of button presses, and p = 0.99. so, if we let X be a random variable that follows that binomial distribution B(n, 0.99), then X corresponds to how many times we win money after pressing the button n times. (e.g., if we “only” get $10,000,000 after n button presses, then X = 1.)
in this setup, the probability of getting a billion dollars is given by
(this is basically just summing up all scenarios in which we get the money outcome at least 100 times.)
to calculate the chance of getting a billion dollars and becoming a woman, notice that we are guaranteed to be a woman so long as we hit the button fewer than n times. so, the probability of getting a billion dollars and becoming a woman is given by
to answer your questions, we just need to find the smallest value of n that makes both of the above equations greater than or equal to 0.90. there are probably some clever math tricks that could be utilized to do this, but i just wrote some python code to do it. the values are:
minimum number of presses for a 90% chance of getting a billion dollars: 102 button presses.
minimum number of presses for a 90% chance of getting a billion dollars and becoming a woman: 230 button presses.
okay so bear with me here.
i’m going to calculate this using the binomial distribution, where n = number of button presses, and p = 0.99. so, if we let X be a random variable that follows that binomial distribution B(n, 0.99), then X corresponds to how many times we win money after pressing the button n times. (e.g., if we “only” get $10,000,000 after n button presses, then X = 1.)
in this setup, the probability of getting a billion dollars is given by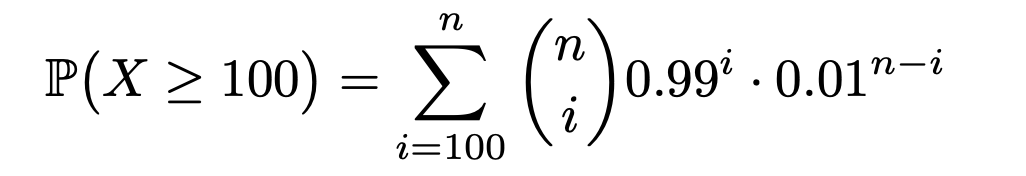
(this is basically just summing up all scenarios in which we get the money outcome at least 100 times.)
to calculate the chance of getting a billion dollars and becoming a woman, notice that we are guaranteed to be a woman so long as we hit the button fewer than n times. so, the probability of getting a billion dollars and becoming a woman is given by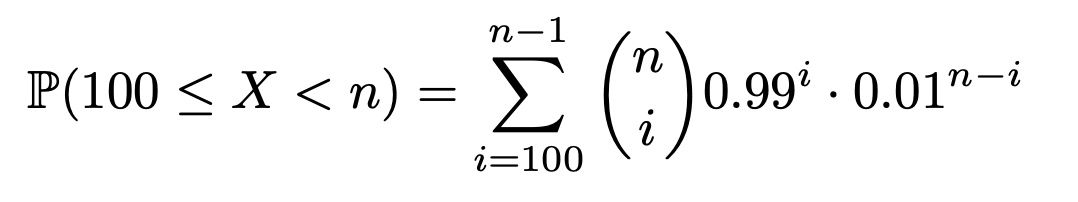
to answer your questions, we just need to find the smallest value of n that makes both of the above equations greater than or equal to 0.90. there are probably some clever math tricks that could be utilized to do this, but i just wrote some python code to do it. the values are:
minimum number of presses for a 90% chance of getting a billion dollars: 102 button presses.
minimum number of presses for a 90% chance of getting a billion dollars and becoming a woman: 230 button presses.
Presses the button 230 times